Сон М.П.,
г. Пермь
УДК 624.943.001.24
НОВЫЙ ПОДХОД К РАСЧЕТУ МНОГОПРОЛЕТНЫХ
И МНОГОЭТАЖНЫХ РАМ НА УСТОЙЧИВОСТЬ
Расчет на устойчивость рамных систем остается актуальной задачей до сих пор, ибо в программных комплексах этот вопрос недостаточно хорошо проработан, а ручной расчет громоздок. Основная трудность заключается в решении системы трансцендентных уравнений, выражающих условие потери устойчивости. Кроме того, в теории устойчивости приняты ряд допущений, поэтому найденное значение критических сил сложно назвать точным. Отсюда следует, какое огромное значение приобретает приближенный расчет. В данной работе разработана методика расчета многоэтажных много-пролетных рам без решения системы уравнений и без построения эпюр.
Теорема: для свободных рамных систем с постоянной высотой стоек значение критической нагрузки остается неизменной, как бы она ни распределялась между стойками рамы.
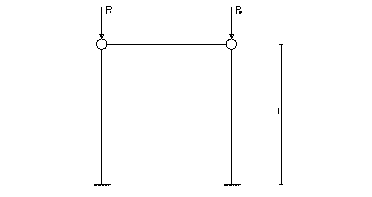
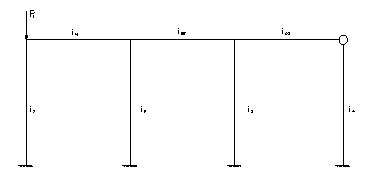
Рассмотрим раму, представленную на рис. 1.

Рис.1. Произвольная рама
Выполним ее расчет на устойчивость методом перемещений. В результате расчета получим уравнение
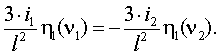 ...........................................................................(1)
...........................................................................(1)
Докажем вспомогательную лемму: принимая линейное смещение рамы за единицу, суммарный момент многопролетной рамы равен критической нагрузке. Вырежем стойки рамы (рис.2).
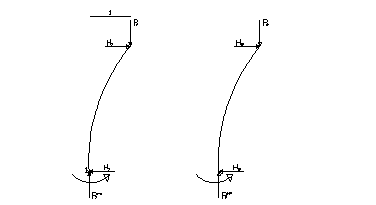
рис 2. Стойки многопролетной рамы
Из условия равновесия вырезанной части (сумма моментов относительно т.1) видно, что момент на опорах равен М = (P1 + P2) · 1 = P, так как Н1 + Н2=0 из уравнения (1).
Соответственно нам не важно, как соотносятся между собой нагрузки Р1 и Р2 при их постоянной сумме. Из вышеизложенного следует, что значение критической нагрузки остается неизменным. Рассмотрим раму с шарнирно закрепленным ригелем, жесткость правой стойки вдвое больше жесткости левой.
Построим график (рис. 3) зависимости критической нагрузки от ее положения на ригеле, понимая, что она распределится обратно пропорционально расстоянию до стоек.
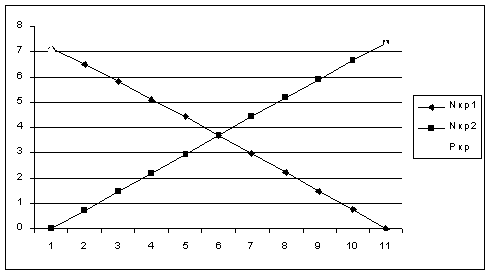
Рис. 3. График зависимости критической силы от ее положения
Ось ординат имеет размерность 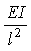 кН. По графику видно, что критическая
нагрузка меняется от
кН. По графику видно, что критическая
нагрузка меняется от 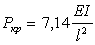 до
до 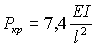 . Соответственно погрешность
не превышает 3,5%.
. Соответственно погрешность
не превышает 3,5%.
Аналогично доказывается теорема и для рамы с жесткими узлами крепления ригеля к стойкам.
После доказательства теоремы становится рациональным искать не критические силы, приложенные в узлах, а критическую нагрузку, которую рама способна вынести до потери устойчивости.
Вспомним, что для балки с двумя жесткими концами, один из которых подвижен,
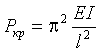 , а для балки с одним свободным
концом
, а для балки с одним свободным
концом 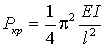 . Эти два случая соответствуют
рамам с бесконечно жесткими ригелями и с шарнирно закрепленными ригелями соответственно
(или ригелями, изгибная жесткость которых равна 0). Таким образом, критическая
нагрузка достигнет максимального значения при жесткости всех ригелей равной
бесконечности и составит
. Эти два случая соответствуют
рамам с бесконечно жесткими ригелями и с шарнирно закрепленными ригелями соответственно
(или ригелями, изгибная жесткость которых равна 0). Таким образом, критическая
нагрузка достигнет максимального значения при жесткости всех ригелей равной
бесконечности и составит
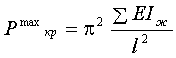 +
+ 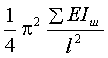 ,
,
где EIж и EIш – жесткости стоек, прикрепленных жестко и шарнирно к ригелю. При уменьшении жесткости ригелей будет уменьшаться и значение критической нагрузки и при жесткости равной 0 составит
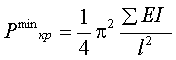 ,
,
где EI – жесткость стоек.
Наша задача найти такую зависимость Pкр от погонных жесткостей ригелей и стоек, чтобы выполнялись все предыдущие рассуждения. Автор предлагает для одноэтажных многопролетных рам пользоваться следующей формулой:
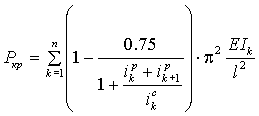 ,..................................................................
(2)
,..................................................................
(2)
где k – номер стойки (ригеля).
Погонные жесткости ригеля суммируются только при жестком сопряжении ригеля с колонной.
Для наглядности рассмотрим несколько примеров.
Пример1.

iр1=1.5i
iр2=2i
i1=1i
i2=1.5i
i3=2.5i
P1=0.5P
P2=0.2P
P3=0.3P
Решая задачу методом перемещений и принимая L = 1, получим систему уравнений:
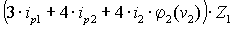 +
+ 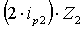 +
+ 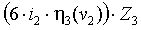 =0
=0
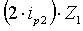 +
+ 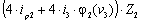 +
+ 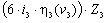 =0
=0
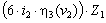 +
+ 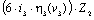 +
+ 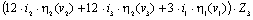 =0
=0
Раскрывая определитель и приравнивая его к нолю, получим v = 3,7648; P1 = 14,18; P2 = 5,67; P3 = 8,5 .
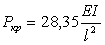 .
.
А теперь решим эту задачу приближенным изложенным выше способом:
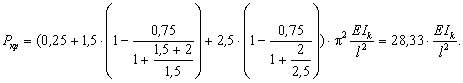
Как видно, погрешность нулевая.
Пример 2.
iр1=2i
iр2=3i
iр2=2i
i1=5i
i2=1i
i3=4i
i4=3i
Решая задачу методом перемещений и принимая l = 1, получим:
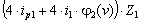 +
+ 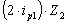 +0+
+0+ 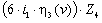 =0,
=0,
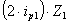 +
+ 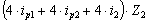 +
+ 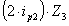 +
+ 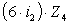 =0,
=0,
0+ 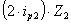 +
+ 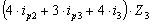 +
+ 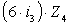 =0,
=0,
 +
+  +
+ 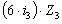 +
+ 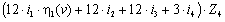 =0.
=0.
Раскрывая определитель и приравнивая его к нолю, получим v = 3,6478.
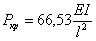 .
.
А теперь решим эту задачу приближенным изложенным выше способом:
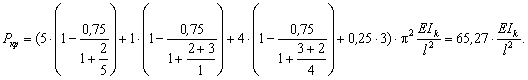
Видно, насколько мала разница точного и приближенного расчетов. Однако при расчете однопролетных рам погрешности несколько возрастут, что пойдет в запас.
При расчете многоэтажных рам устойчивость всей конструкции определяется устойчивостью нижнего этажа. И для рам, у которых нагрузка постоянна на каждом этаже, справедлива следующая формула, которая аналогична формуле (2), но учитывает работу стоек вышележащих этажей, находящихся под нагрузкой:
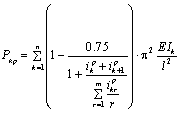 ...............................................................................
(3)
...............................................................................
(3)
Как видно, предложенный способ расчета многопролетных много-этажных рам на устойчивость обладает высокой точностью и малой трудоемкостью.
Литература